感染症拡散シミュレーション
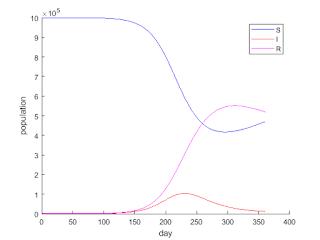
新型コロナウイルス(COVID-19)が日本で拡がっています,心配です。 感染者数変化に関する簡単なシミュレーションを行ってみました。 なお,筆者は医者ではありませんし,感染症を専門に研究しているわけでもありません。 過去に水を伝って広がる感染症(水系感染症)に関する研究を一時期やったことがあるので,その知識を応用してみました。 一部的外れな議論があるかもしれません。 (計算条件) まだこのウイルスに関する詳細な情報がないので,パラメータは適当に設定。 感染確率(※)を3つに変化させて計算。 ※既に感染している人から,他の人に感染する確率。 人口 100万人の都市を想定。 感染から回復したあとしばらくの期間は免疫を獲得し再び感染することはないが,その後再び感染する可能性のある状態に戻る。 図中,S(青),I(赤),R(マゼンタ)は,それぞれ健康な人(感染の可能性のある人),感染者(症状のない人も含),回復した人の数を表しています。 感染確率が小さい場合は,感染者数が最大になるまでの日数が長くなり,感染者数の最大値も小さくなります。逆に,確率が大きいと日数が短くなり,感染者数の最大値は大きくなります。 中国では既に患者数増加の程度が小さくなってきているので,感染者が出始めておよそ2〜3ヶ月で感染者数は最大になるようです。 このことを考えると,今回計算した3つのケースの中では,ケース3(感染確率が最も大きい場合)が時間的には近くなります。 ケース3の結果では,最初の感染者が出て約60日後に全住民の4割ほどの人が同時期に感染し,その後次第に回復しています。 この時,都市のほとんどの人が感染している(状態 I)か,あるいは回復して再び感染することはない状態(状態 R)になっていて,感染する可能性がある状態(S)の人がほとんど残っていないため新たな感染が起こりにくくなり,結果として感染者数は減少していく結果となっています。 ただ,WHOの統計によると,中国・湖北省での感染者数(累積)は,ほぼピークである現在でも人口の0.1%ほどしかありません。 と言うことは, 患者の隔離など,拡散防止策が有効に機能している か, 感染したけど症状の出ない人が多数いる か, 感染しやすい人と,しにくい人に分かれ...
